概率基础

概率密度函数

概率密度函数与概率分布函数

$$P(a<x<b)=\int_a^bp(x)dx$$

$P(a<x<b)$表示$x$落在区间$[a,b]$之间的概率。当$a\rightarrow \infty, b\rightarrow +\infty$时，有

$$\int_a^bp(x)ds=1$$

概率密度估计

概率密度估计可以分为参数方法与非参数方法。参数方法是指假设给定数据服从某一个已知的分布类型，用得到的样本值对该分布的相关参数作出估计，即得到对应的概率密度函数。参数方法的优点是不需要许多的样本就可以对概率密度作出估计，缺点是如果未知的概率分布过于复杂，与已知的概率分布类型不合，会造成效果不好。而非参数方法，又称为核密度估计（Kernel Density Estimation）方法，不需要对潜在的概率分布模型作出假设，而是自动地从数据中学习获得。其缺点是需要大量的样本，而且随着维数的增长，会带来“维数灾难”的问题。下面介绍非参数估计方法。

非参数估计方法的主要思想是：通过一个样本周围的小区域$\mathcal{R}$的概率来估计$p(x)$。

假设$\mathbf{x}$的概率密度为$p(\mathbf{x})$，则任一$\mathbf{x}$落入区域$\mathcal{R}$的概率为

$$P=\int_{\mathcal{R}}p(\mathbf{x})d\mathbf{s}$$

假设$n$个独立同分布（i.i.d）的样本中有$k$个落在区域$\mathcal{R}$中的概率为$P_{k}=C_{n}^{k} P^{k} (1-P)^{n-k}$则$k$的期望值为$E(k)=np$。当数据量$n$很大时，$P_k$在$nP$附近有非常显著的尖峰，可以用$k$的观察值代替$E(k)$。从另一个角度看，这里使用频率估计概率，即

$$P=\frac{E(k)}{n}\approx \frac{k}{n}$$

当$n\rightarrow \infty$时，可以保证频率与概率相等的概率为1（伯努利大数定律）。在曲线图上看来就是一个$\delta$函数，这样保证估计结果就是真正的概率。根据积分中值定理，存在$\mathcal{R}$中的某个点$\mathbf{x}^\prime$，使得

$$P=\int_{\mathcal{R}}p(\mathbf{x})d\mathbf{x}=p(\mathbf{x}^\prime)V$$

其中$V=\int_{\mathcal{R}}d\mathbf{x}$是区域$V$的大小的度量。如果$\mathcal{R}$足够小，使得$p(\mathbf{x})$在$\mathcal{R}$中的变化特别小，则有$P\approx p(\mathbf{x})V$，其中$\mathbf{x}$是$\mathcal{R}$中的任意一点。于是有

$$p(\mathbf{x})=\frac{P}{V}=\frac{k/n}{V}$$

在样本数量有限的情况下：

$V$过大：得到空间平滑后的$p(\mathbf{x})$。
$V$趋近于0：
1. 如果$\mathcal{R}$中没有样本点，则$p(\mathbf{x})=\frac{k/n}{V}=0$。
2. 如果$\mathcal{R}$内碰巧有一个样本，则$p(\mathbf{x})=\frac{k/n}{V}\approx\infty$。

假设样本有无限多个，构造一系列包含$\mathbf{x}$的区域$\mathcal{R_1},\mathcal{R_2},…$，其中$\mathcal{R_1}$使用一个样本，$\mathcal{R_2}$使用两个样本，则使用$R_n$得到的估计为

$$p_n(\mathbf{x})=\frac{k_n/n}{V_n}$$

其中$k_n$表示落入$\mathcal{R_n}$中的样本个数，$V_n$表示$\mathcal{R_n}$的体积。为了使得$\lim\limits_{n\to\infty}p_n(\mathbf{x})=p(\mathbf{x})$，必须满足一下条件

$\lim\limits_{n\to \infty}V_n=0$
$\lim\limits_{n\to \infty}k_n=\infty$
$\lim\limits_{n\to\infty}k_n/n=0$

其中有两种方法获得这种区域序列。一种是根据确定的体积函数，比如$V_n=\frac{1}{\sqrt{n}}$，来逐渐收缩到一个给定的初始区间，即Parzen窗方法。另一种是确定$k_n$为$n$的某个函数，如$k_n=\sqrt{n}$，即$K_n$-邻近方法。

Parzen窗方法

假设$\mathcal{R}$是边长为$h$的$d$维超立方体，则$\mathcal{R_n}$的体积为$V_n=h_n^d$。定义如下窗函数

$$\varphi(\mathbf{u})= \begin{cases} 1,&\vert u_i\vert\leq1/2,\forall i\in[1,d]\\ 0,&otherwise\ \end{cases}$$

这样$\phi(\mathbf{x})$就表示在一个中心在原点的单位超立方体。如果$\mathbf{x}_i$落在超立方体中，则$\varphi(\mathbf{x}_i)=1$，否则$\varphi(\mathbf{x}_i)=0$。假设$\mathbf{x}$是$\mathcal{R_n}$的中心，如果$\mathbf{x}_i$落入$\mathcal{R_n}$中，则有$\varphi(\frac{\mathbf{x}-\mathbf{x}_i}{h_n})=1$。超立方体$\mathcal{R}_n$中的样本个数为

$$k=\sum_{j=1}^n\varphi\left(\frac{\mathbf{x}-\mathbf{x}_j}{h}\right)$$

用$n$个样本来近似$p(\mathbf{x})$，有

$$p(\mathbf{x}) \approx \hat{p}{n}(\mathbf{x}) = \frac{k/n}{V} = \frac{1}{n} \sum{j=1}^{n} \frac{1}{V} \varphi(\frac{ \mathbf{x}- \mathbf{x}_{j}}{h})$$

定义

$$\delta(\mathbf{x})=\frac{1}{V}\varphi\left(\frac{\mathbf{x}}{h}\right)$$

则对$p(\mathbf{x})$的近似可以重写为$p(\mathbf{x})=\frac{1}{n}\sum_{j=1}^n\delta(\mathbf{x}-\mathbf{x}_j)$

其中$\delta \left(\mathbf{x}-\mathbf{x}{j}\right)$表示插值函数，即每个样本$\mathbf{x}{j}$都对$p(x)$的估计产生一定的贡献，这种贡献根据 $\mathbf{x}{j}$到$\mathbf{x}$的距离，通过某种形式的插值函数表现出来。由于$\varphi(\mathbf{u})\geq 0$且$\int\varphi(\mathbf{u})d\mathbf{u}=1$，所以 $$\hat{p}{n}(\mathbf{x})=\frac{1}{n}\sum_{j=1}^{n}\frac{1}{V}\varphi\left(\frac{\mathbf{x}-\mathbf{x}{j}}{h}\right)\geq 0$$ 以及 $\int\hat{p}{n}(\mathbf{x}) d\mathbf{x}=\frac{1}{n}\sum_{j=1}^{n}\frac{1}{V}\varphi\left(\frac{\mathbf{x}-\mathbf{x}{j}}{h}\right) d\mathbf{x}=\frac{1}{n}\sum{j=1}^{n}\frac{hd}{V}\int\varphi(\mathbf{u}) d\mathbf{u}=1$。

这说明估计得到的$\hat{p}(\mathbf{x})$是一个合理概率密度函数，且其离散型和$\varphi(\mathbf{x})$保持一致。

下面是$h$对$\hat{p}_n(\mathbf{x})$的影响：

$h$非常大时，$\mathbf{x}_i$到$\mathbf{x}$的距离对$\delta(\mathbf{x}-\mathbf{x}_j)$的影响不大
- $\hat{p}_n(\mathbf{x})$为$n$个宽的、慢的函数相加
- $\hat{p}_n(\mathbf{x})$是对$p(\mathbf{x})$的非常平滑的估计——散焦估计
- 估计结果的分辨率低
$h$非常小时，$\delta(\mathbf{x}-\mathbf{x}_j)$的峰很尖锐
- $\hat{p}_n(\mathbf{x})$为$n$个以样本点为中心的尖脉冲的叠加
- $\hat{p}_n(\mathbf{x})$是对$p(\mathbf{x})$的充满噪声的估计
- 估计结果的统计稳定性不足

所以在有限样本数目的约束下，$h$（或$V$）应取某种可接受的折中，并且随着$n$的增大，$h$（或$V$）应该逐渐减小，以使得对$p(\mathbf{x})$的估计更为精确。另外可以对窗函数做以下泛化：不必规定$\mathcal{R}$为超立方体，而是某种由窗函数定义的一般化的形式，仅需窗函数满足$\varphi(\mathbf{u})\geq 0$且$\int\varphi(\mathbf{u})d\mathbf{u}=1$，以使得$\hat{p}_n(\mathbf{x})$为一个合理的概率密度函数。

Parzen方法的优点是：①通用性：不必了解分布的形式就能对其作出估计；②在训练样本足够多的情况下，无论实际的概率密度函数的形式如何，最终肯定能得到一个可靠的收敛的结果。缺点是：①需要大量的训练样本，往往比已知分布的参数形式而进行参数估计所需的训练样本个数多得多；②“维数灾难”对训练样本个数的需求，随着特征空间的维数指数增长。

此外，如果$p(\mathbf{x})$的分布不均匀，Parzen方法在整个特征空间中采用的同样的窗宽度可能无法总是得到一个令人满意的结果。解决该问题的一个思路是：不固定窗宽度，二是固定包括在$\mathbf{x}$周围的每个区域的样本数$k$。通常$k$取决于样本总数$n$，所以表示为$k_n$，当$\mathbf{x}$周围数据密度大时，窗口变小（分辨率高），当$\mathbf{x}$周围数据密度小时，窗口变大（分辨率低），包括进来的$k_n$个样本称为$\mathbf{x}$的$k_n$最近邻点。

Python仿真

import numpy as np
import matplotlib.pyplot as plt

def gaussian_pdf(x, mu, sigma):
    prob = 1/np.sqrt(2*np.pi)/sigma*np.exp(-(x-mu)**2/2/sigma**2)
    return prob

def parzen_window_pdf(x, data, sigma):
    px = [gaussian_pdf(x, mu=mu, sigma=sigma) for mu in data]
    return np.mean(np.array(px), axis=0)

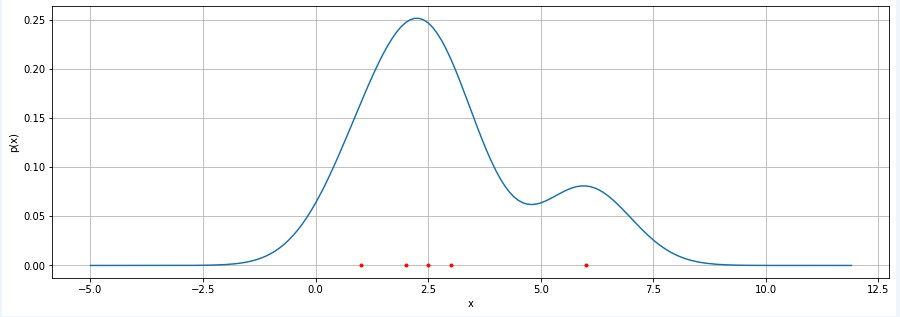
data = [2, 2.5, 3, 1, 6]
x = np.arange(-5, 12, 0.1)
prob = parzen_window_pdf(x, data, sigma=1)
plt.figure(figsize=(15,5))
plt.plot(x, prob)
plt.plot(data, [0]*len(data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.show()